Techno’s
“Know your car” Series #11
Mazda MX-5 Piston Acceleration
And Piston Velocity
Introduction
This
3-part article is about the piston and crankshaft movements in the Mazda MX-5
1.6 and 1.8 litre engines. The purpose is to expose the stresses and strains
upon the piston, connecting rod and crankshaft during acceleration and at
particular rpm's.
The
principles and algorithms used in this article can be applied to any 4-stroke
engine. To assist the reader to understand the calculations I have included the
more complex algorithms for reference.
Part 1 - The Basics
Mazda
has made two basic engines for the MX-5; the 1.6 litre and the 1.8 litre. In
Table 1 contains the base data used in the article. The values
in the shaded cells are the primary data used in the calculations for the other
values.
Table
1 MX-5 Engine Specifications
|
Model Description |
Ref. Value |
MX-5 1.6 litre |
MX-5 1.8 litre |
||
|
Stroke mm |
S |
83.6 |
85.0 |
||
|
Bore mm |
B |
78.0 |
83.0 |
||
|
Connecting Rod Length (+/- 0.05mm) |
R |
132.90 |
132.90 |
||
|
Number of Cylinders |
N |
4 |
4 |
||
|
Bore Stroke ratio |
B/S |
0.933014 |
0.976471 |
||
|
Stroke Bore ratio |
S/B |
1.071795 |
1.024096 |
||
|
Rod Stroke ratio |
R/S |
1.589713 |
1.563529 |
||
|
Displacement per cylinder (cc) |
D[i] |
399.47 |
459.90 |
||
|
Engine Displacement (cc) |
D*N |
1597.88 |
1839.61 |
||
|
Crank Arm mm |
S/2 |
41.8 |
42.5 |
||
|
Other Variables
Used in the Algorithms |
|||||
|
RPM |
T |
Revolutions per minute of the
Crank |
|||
|
Picton Velocity |
V |
This is the speed of the
Piston's movement measured in meters per second |
|||
|
Piston Acceleration |
A |
The rate of change in
velocity, measured in meters per second per second |
|||
|
Crank Angle |
K |
Crank angle in degrees after
TDC |
|||
Table
1 contains all the data used in the calculations. The column titled "Ref
Value" contains the variables assigned various components in the
algorithms. In the worked examples I have used the 1.8 litre engine and 6,000
rpm as a benchmarks for illustrations. To enable the formula to be Excel
computable I have used Excel functions such as "SQRT",
"ATAN" and "^", etc.
Understanding
the Piston, Rod and Crank Arrangement
To
understand the data contained in this article it is useful to be able to
identify the parts of the engine being discussed. Figures 1,2 and 3 display the
movement and relationships of the components.
Reference
to TDC and BDC are explained in relation to the piston's location and the
stages in the rotation of the crank.
|
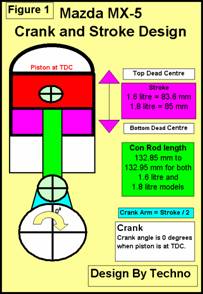
Figure1 Piston at Top Dead Centre (TDC)
Figures 1 shows the piston
(red) at top dead centre (TDC). This is the highest position of the piston
and occurs when the con-rod (green) and crank arm (blue) both fully extended.
The crankshaft (white) is at zero degrees and ready to start a 360-degree
revolution. |
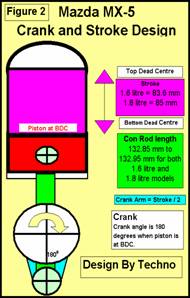
Figure 2 Piston at Bottom Dead
Centre (BDC)
Figure 2 shows the piston at bottom dead centre. The
crank has turned 180 degrees the piston has travelled one stroke and is at
its lowest point, called bottom dead centre (BDC). When the piston is in this position the con-rod is
vertical and the crank arm is facing downward. |
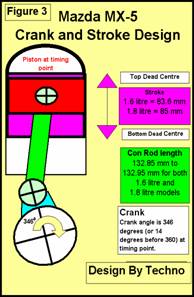
Figure 3 Piston Approaching TDC
Figure 3 Shows 1.
The con-rod links
the piston to the crank arm. 2.
The con-rod and
crank arm geometry translates the vertical movement of the piston into a
rotating motion of the crankshaft. 3. The length of the con-rod and crank arm
determine the stroke travel of the piston. |
Figure 3, while demonstrating the relationships of the components in
motion also shows the location of the piston when passing a timing point, in
this case 14 degrees before TDC.
There
are 360 degrees in one rotation of the crankshaft. When the timing is at 14 degrees before TDC
the spark is fired at 346 degrees of rotation of the crank. Imagine the end of
the crank being a clock dial with 12 o'clock being 0 degrees. At 14 degrees
BTDC the clock would be at 11.57 and 20 seconds.
Part 2 - The
Movement of The Piston
During
one 360 revolution of the crank in a MX-5 1.8 litre engine the piston:-
·
travels down 85.0 mm
(TDC to BDC); stops
·
travels up 85.0mm
(BDC to TDC); and stops
When
the engine is turning over at 6,000 rpm the piston travels down 6,000 times per
minute and up 6,000 times per minute. Therefore, at 6,000 rpm piston travels
12,000 x 0.85m = 1,020 meters per minute, or as is more widely use, 17.0 meters
per second (1,020/60). Since the piston
stops at each 180-degree rotation of the crank then 17.0m per second is the
average, or mean, speed of the piston. So what is the velocity of the piston at
during its movement?
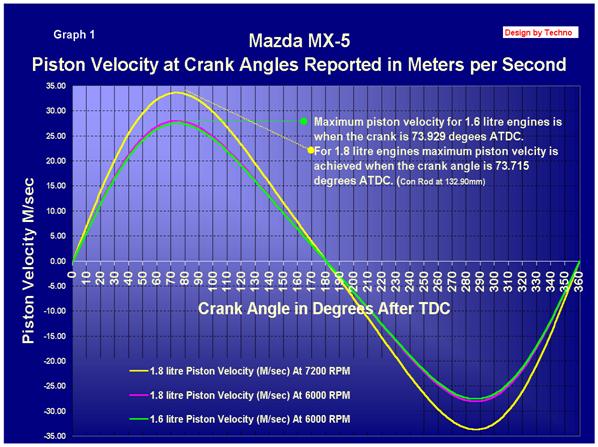
Graph
1 plots the velocity of the
piston at 10-degree intervals over one revolution or the crank. Notice how the
maximum velocity is reached when the crank angle is around 74 degrees ATDC.
This is very close to the position when the crank arm and the con-rod form a
90-degree angle. The maximum piston velocity, in the 1.8 litre is reached at
when the crank angle is 73.715 degrees after TDC.
Graph
1 Piston Velocity
Graph
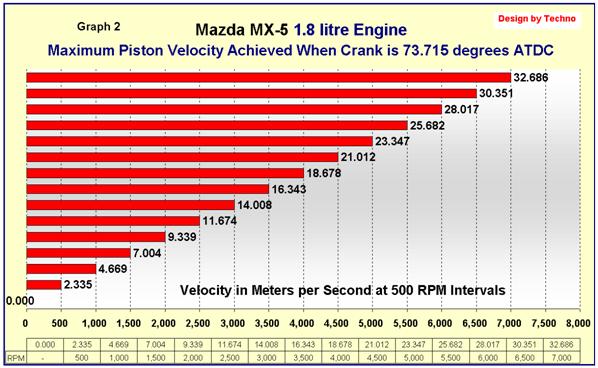
2 shows the (Maximum) Piston
Velocity of a 1.8 litre MX-5 piston as it passes the 73.715-degree mark ATDC,
in 500 RPM increments.
Graph
2 Maximum Piston Velocity
Graph
3 shows the acceleration rate of
the piston over one full crank rotation. The velocity of the piston is a
consequence of the rate and duration of acceleration of the piston.
Acceleration (A) is measured in meters per second per second.
Graph
3 Piston Acceleration
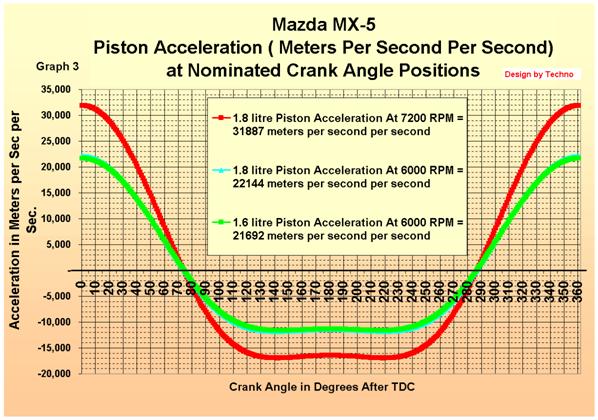
Note from the graph
·
the maximum
acceleration rate is achieved immediately before and after TDC, and
·
the acceleration
rate goes from positive to negative at around 74 degrees after TDC. This is
immediately after the highest velocity reading is obtained and the piston is
now slowing (and reverses at 286 degrees (ie 74 Before TDC)).
Table 2 shows the piston acceleration (A) for the 1.6 litre and
1.8 litre engines at 500 RPM intervals and compares that to the 1,000 RPM index
value. The acceleration rate is recorded at the commencement of movement at
TDC, which is the greatest acceleration rate at any time in the crank rotation.
The piston acceleration of a 1.8 litre engine is a constant 1.02082 times the
1.6 litre because of the increased stroke length. Notice how a doubling of the
RPM creates a squaring of the acceleration rate. The piston of a 1.6 litre
Mazda MX-5 engine accelerated at 603 meters per second per second at 1,000 rpm.
This acceleration rate is 4 times that at 2,000 RPM, 16 times at 4,000 RPM and
36 times at 6,000 RPM. In the 1.8 litre the g forces at 7,200 RPM are 64 times
that at idle (900 RPM).
Table
2 Maximum
Piston Acceleration Rate at Modelled RPM in Meters Per Second Per Second
|
RPM |
Mazda MX-5 1.6 Litre 83.6 mm Stroke |
Mazda MX-5 1.8 Litre 85 mm Stroke |
Relationship to Acceleration at
1,000 RPM |
|
1,000 |
603 |
615 |
1.00 |
|
1,500 |
1,356 |
1,384 |
2.25 |
|
2,000 |
2,410 |
2,460 |
4.00 |
|
2,500 |
3,766 |
3,844 |
6.25 |
|
3,000 |
5,423 |
5,536 |
9.00 |
|
3,500 |
7,381 |
7,535 |
12.25 |
|
4,000 |
9,641 |
9,842 |
16.00 |
|
4,500 |
12,202 |
12,456 |
20.25 |
|
5,000 |
15,064 |
15,378 |
25.00 |
|
5,500 |
18,227 |
18,607 |
30.25 |
|
6,000 |
21,692 |
22,144 |
36.00 |
|
6,500 |
25,458 |
25,988 |
42.25 |
|
7,000 |
29,526 |
30,140 |
49.00 |
|
7,500 |
33,894 |
34,600 |
56.25 |
|
8,000 |
38,564 |
39,367 |
64.00 |
Note that the acceleration rate
at 6,000 rpm is 4 times that at 3,000 RPM
and a 20% increase in RPM from
6,000 to 7,200 results in a 44% increase in the acceleration rate of the
piston.
There are 101.9716 gravitational
acceleration units "g forces" per 1,000 meters per second per second
acceleration. Therefore, at 6,000 RPM, when the 1.8 litre engine's piston has a
maximum acceleration rate of 22,144 m/s/s there are 2,258.06 "g
forces" exerted. Small wonder that lightweight pistons and con-rods are
the order of the day on high performance engines.
Part 3 - Location and
Displacement of the Piston at Crank Angles.
Each piston in the 1.8 litre
engine strokes 85mm, and with an 82mm bore, displaces a volume of 459.902 cc's.
Because of the geometry of the rod and crank arm the movement of the piston in
the cylinder is bell shaped when plotted on a graph.
Graph 4 shows the graph shows the location of the piston in mm
from TDC at various crank angles (scaled to the left side of the graph) and the
displacement at crank angles (scaled to the right side).
Graph 4 Piston Location and
Displacement
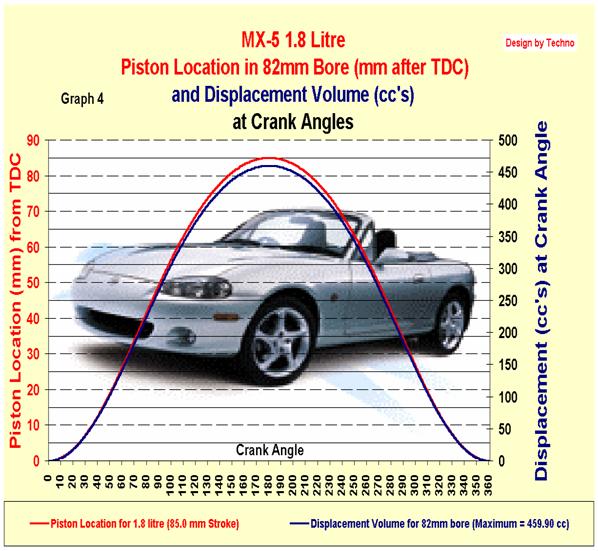
Table 3 shows the location of the top of the piston in the bore
for the 20 degrees of crank rotation approaching Top Dead Centre (TDC).
Table 3 Location of Piston
Top for 20 Degrees of Rotation Before TDC
|
Crank Angle Before TDC |
MX-5 1.6 litre piston location
in mm from TDC |
MX-5 1.8 litre piston location
in mm from TDC |
|
Crank Angle Before TDC |
MX-5 1.6 litre piston location
in mm from TDC |
MX-5 1.8 litre piston location
in mm from TDC |
|
-20 |
3.2920 |
3.3604 |
|
-10 |
0.8334 |
0.8507 |
|
-19 |
2.9759 |
3.0377 |
|
-9 |
0.6756 |
0.6896 |
|
-18 |
2.6750 |
2.7306 |
|
-8 |
0.5342 |
0.5453 |
|
-17 |
2.3896 |
2.4392 |
|
-7 |
0.4092 |
0.4178 |
|
-16 |
2.1196 |
2.1637 |
|
-6 |
0.3008 |
0.3071 |
|
-15 |
1.8654 |
1.9041 |
|
-5 |
0.2090 |
0.2134 |
|
-14 |
1.6269 |
1.6607 |
|
-4 |
0.1338 |
0.1366 |
|
-13 |
1.4044 |
1.4336 |
|
-3 |
0.0753 |
0.0769 |
|
-12 |
1.1979 |
1.2228 |
|
-2 |
0.0335 |
0.0342 |
|
-11 |
1.0075 |
1.0285 |
|
-1 |
0.0084 |
0.0085 |
|
|
|
|
|
TDC |
0.0000 |
0.0000 |
Notice
the difference between the 1.6 litre and 1.8 litre models. This is because the
1.8 litre (85mm) has a longer stroke than the 1.6 litre (83.6mm).
The
shaded lines at -10 and -14 degrees before TDC show the location of the
piston's top at the popular timing point alternatives for the 1.6 litre models.
A 4-degree advance in the timing is a 40% change in degrees BTDC and a 95.21%
increase in the distance (in mm) travelled by the piston from the timing point
and TDC.
The effect
this has on the engines' performance is discussed in Techno's “Know your car
Series #10: What Happens When the Timing Is Advanced".
The Definitive Guide to Piston
and Crank Movement.
Table 4 shows the comparisons between the 1.6 litre and the 1.8
litre engines running at 6,000 rpm.
Table 4 Comparison of 1.6 litre
and 1.8 Litre Engines at 6,000 RPM
|
Data |
1.6 Litre |
Ref Value |
1.8 Litre |
|
Revolutions per minute at 6,000 RPM |
6,000 |
T |
6,000 |
|
Revolutions Per Second at 6,000 RPM |
100.00 |
T/60 |
100.00 |
|
Degrees rotation per second at 6,000 RPM |
36,000 |
360*(T/60) |
36,000 |
|
Milliseconds Per Revolution at 6,000 RPM |
10.00 |
1/(T/60)*1000 |
10.00 |
|
Milliseconds per degree at 6,000 RPM |
0.02778 |
1/(360*T/60)*1000 |
0.02778 |
|
Maximum Piston Acceleration (Positive) (Gmax meters per second squared)
at 6,000 RPM |
21,692 |
((T^2*S)/182.38)*(1+1/(2*(R/S)))/1000 |
22,144 |
|
Maximum Piston Deceleration in meters per second squared at 6,000 RPM |
- 11,597 |
A Plotted |
- 11,761 |
|
Time for Piston to Move from Timing mark (10) to TDC
(Milliseconds) at 6,000 RPM |
0.2778 |
10/(360*T/60)*1000 |
0.2778 |
|
Piston travel from Timing Point to TDC (mm) at 6,000 RPM |
1.62692 |
W when K = 360 minus W when K = 350 |
1.66074 |
|
Mean Piston Speed Meters Per Second at 6,000 RPM |
16.720 |
((S/1000)*T*2)/60 |
17.000 |
|
Mean Piston Speed (Kph) at 6,000 RPM |
60.192 |
((S/1000)*T*2)*60 /1000 |
61.200 |
|
Maximum Piston Speed at 6,000 RPM (Meters per Second) |
27.542 |
V |
28.047 |
|
Maximum Piston Speed at 6,000 RPM (Kms per hr) |
99.15 |
V*60*60 /1000 |
100.97 |
Summary
Congratulations,
you have made it this far through this article, well done. Now you should have
an understanding of the movements of a piston, con-rod and crank. The forces
that act on the components are indeed impressive and help us to understand just
how complex engines are, and the engineering developments required to design
and build reliable engines that last for 300,000 Kms or more.
Safe
journey
Rob
(Techno) Spargo
January
2004
Formulae for Calculations in
Excel Format
The
tables above provide the explanations for the lettered variables
To
calculate the velocity (V) of the piston when the crank is at a particular
degree of rotation (K) ATDC and at a given RPM (T) the formula is:
Piston Velocity at a given crank
angle
V=(T*ATAN(1)/7.5)*((S/2)/1000)*SIN(((ATAN(1)/7.5)*K/6))*(1+COS(((ATAN(1)/7.5)*K/6))/(SQRT(((R/(S/2))^2)-SIN(((ATAN(1)/7.5)*K/6))*SIN(((ATAN(1)/7.5)*K/6)))))
The formula for calculating the
acceleration rate (A) of a piston at a given crank angle after TDC (K) is
Acceleration in
Meters per second per second at K
=((T*ATAN(1)/7.5)^2)*((S/2)/1000)*
((1-COS(4*((ATAN(1)/7.5)*K/6)))/(8*(SQRT(((R/(S/2))^2)-SIN(((ATAN(1)/7.5)*K/6))*SIN(((ATAN(1)/7.5)*K/6))
))^
3)+COS(2*((ATAN(1)/7.5)*K/6))/(SQRT(((R/(S/2))^2)-SIN(((ATAN(1)/7.5)*K/6))*SIN(((ATAN(1)/7.5)*K/6))
))+COS(((ATAN(1)/7.5)*K/6)))
The
formula for the location (W) and displacement (D) of the piston for a given
crank angle (K) after TDC is:
Location = W =
(((S/2)+R)-((S/2)*COS(RADIANS(K)))-SQRT(R^2-((S/2)*SIN(RADIANS(K)))^2))
Displacement at K =
D =
(+PI()*(B^2)*W/1000)/4