| prev | home | next |
Brian Beckman, PhD
ęCopyright March 2001
Trail-braking is a subtle driving technique that allows for later braking and increased corner entry speed. The classical technique is to complete braking before turn-in. This is a safer, easier technique for the driver because it separates traction management into two phases, braking and cornering, so the driver doesn't have to chew gum and walk at the same time, as it were. With the trail-braking technique, the driver carries braking into the corner, gradually trailing off the brakes while winding in the steering. Since braking continues in the corner, it's possible to delay its onset in the preceding straight braking zone. Since it eliminates the sub-optimal moments between the ramp-down from braking and the ramp-up to limit cornering by overlapping them, entry speeds can be higher. The combination of these two effects means that the advantage of later braking is carried through the first part of the corner. In many ways, this is the flip side to corner exit, where any speed advantage due to superior technique gets carried all the way down the ensuing straight. The magnitude of the trail-braking effect is much smaller, though: perhaps a car length or two for a typical corner. Done consistently, though, it can accumulate to whole seconds over a course.
When I was taught to drive in the '80s, not all the fast drivers used trail braking and instructors usually gave it at most a passing mention as an optional, advanced technique. The reason was probably a risk-benefit analysis:
Another reason may have been that my instructors hadn't got their butts kicked recently by a trail-braking driver. It was not a commonplace technique back then, so one might drive a whole season of club racing without getting spanked by trail braking. Since not everyone used it, not everyone had to develop the skill.
Nowadays, however, the general level of driving skill has increased to the point where it's no longer optional, unless you're content with fourth place.
As with most driving skills, it's difficult to get a feel for the limits without exceeding them from time to time. However, exceeding the limits at trail braking has some of the worst consequences one can invite on a race track, typically worse than those from mistakes at corner exit. It's definitely a big risk for a small effect, justified only because it accumulates. Blowing it results in too high an entry speed. You get:
That's one of the reasons I have not, in the past, singled it out for my personal driver-development work - it's hard to do at all and harder to do it consistently and just didn't seem worth it. Another reason is that the kinds of cars I like to drive let you get away without it much of the time. I prefer ultra-powerful cars because they're fun and loud and attract a lot of attention. Paradoxically, though, such cars can lull one into becoming a lazy driver. With a lot of power on tap, you can often make up for an overly conservative entry speed on the exit.
However, when the cars are equalized, as in spec races, showroom stock, or in a lot of Solo II car classes, trail braking takes a prominent role. It can be difficult to spot it as an issue in Solo II, where drivers are alone against the clock. All else being equal, a Solo II driver without trail braking may just find himself scratching his head wondering how in blazes the other drivers can be so much faster. Go wheel-to-wheel on the track with equal cars, though, and the issue becomes instantly and visually obvious. You may be just as fast in the corner, coming out of the corner, down the straight. You may have perfect threshold braking. You may have perfect turn-in, apex and track out points. But that little extra later braking and entry speed will allow the trail-braker to take away several feet every corner. Corner after corner, lap after lap, he will gobble you up.
I recently completed a road-racing school at Sebring International Raceway where this is precisely what I saw. In identical Panoz school cars, the drivers who were faster than I were doing it right there and nowhere else. My ingrained, outdated style did me in, and even though I had much, much more on-track experience than the rest of the students, and even though they weren't faster in top speed than I, and even though their cornering technique was not nearly as polished as mine, three (out of twelve) of them had better lap times than I.
The instructors were as surprised as I. One even said he would have bet money that I was the quickest from watching me and riding with me (instructors sis not ride in the wheel-to-wheel sessions). The clock doesn't lie though, and we were scratching our heads and I started swapping cars. Once we went wheel-to-wheel on the third day of the program, I spotted it, right there the first time into turn 2: the three quicker drivers took a car length from me on the corner entry. They did it again in turn 10 (Cunningham), at the Tower turn, and turn 15 approaching the back stretch: all the turns requiring full braking and downshifts. I made up a bit at the hairpin, which is an autocrosser's corner if there ever was one, and I knew the importance of not missing the apex by more than an inch or two if possible. They also couldn't beat me entering turn 17, which has no straight braking zone: instead, the best technique is to brake partially after turn in (at 115 mph, this is big-time, serious fun). Thus, turn 17 did not trigger my old-fashioned "braking-zone" program, and I was able to use my high-speed experience to coax a bit more than average grip through it. So, in sum, my conservative turn-ins on the slow corners added up to about half a second per lap, which is about 65 feet at the start-finish line where we're going about 90 mph =132 fps (90 x 22 / 15). Ugly.
I was doing it the old-fashioned way: get the braking done in the braking zone and get your foot back on the gas pedal and up to neutral throttle before turn-in. That little tenth of a second or so where I'm coasting and they're still braking is the car-length they were taking out on me. It was small enough that the instructors couldn't feel it or see it. But electronic instrumentation would have picked it up. When I go back to the Panoz Sebring school next year, I will take advanced sessions in fully instrumented cars, where the instructors go out for some laps at 10/10s, then the students go out in the same car and take data. Back in the pits, the charts are differenced and the student can see precisely what he needs to do to come up to the instructor's level (most of the instructors have years of experience on the track, and hold current or former lap records in various cars on the course, so it's quite unlikely that a student will be as quick out of the box).
The following is a picture of the course snipped from the web site at http://www.sebringraceway.com/, so you can see the bits of the course I'm talking about:
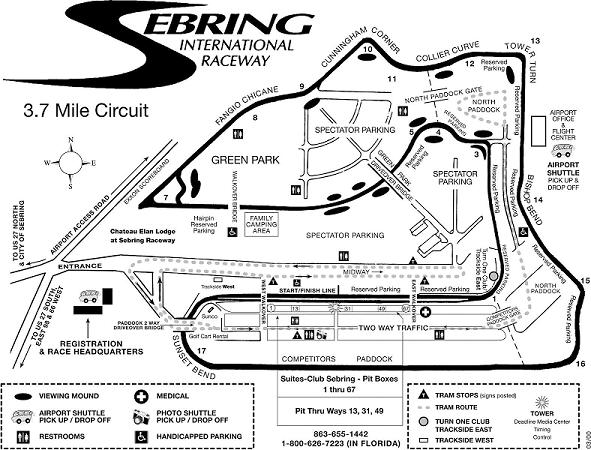
Let me say a few things about the school. The three-day program consisted of
It's a great program, easily better than spending the same amount of money on the car: highly recommended.
Sebring is large, exciting, lovely, complex course with a deep history of sports-car racing. It is currently 3.70 miles in length, though it has been as long as 5.7 miles in its history. Let's do some dead reckoning, that is, math in our heads without even envelopes to write on. We'll see if we can cook up some data, from memory, to justify the intuitions and explain the results above.
There are 2.54 centimetres per inch: that's an exact number. Therefore, there are 2.54 x 12 = 30.48 centimetres per foot. The number of centimetres per mile, then are 30.48 x 5280 = 30 x 52 x 100 + 30 x 80 + 48 x 52 + 48 x 80 / 100 = 156000 + 2400 + (50 - 2)(50 + 2) + 3840 / 100 = 158400 + 2500 - 4 + 38.40 = 160,934.4. Thus, a mile contains 1.609344 kilometres, which we can round to 1.61, which is, conveniently, 8/5 + 1/100. So 3.70 miles is 29.637 / 5 = 5.927 kilometres or just about 6. Now, there are 5280 / 3 = 1760 yards in a mile, so we have 3700 + 2590 + 222 = 6,512 yards, which is consistent with 6 kilometres, so we've got a check on our math. In fact, we can be a little more sanguine about it. Another number we remember is that there are about 39 inches per metre; that's a yard and three inches, or 13/12 yard. So, if we have about 6,000 metres, that's going to be about 6,000 + 6,000 / 12 = 6,500 yards. Amazing, isn't it? Finally, this is 6,512 x 3 = 13,036 + 6,512 = 19,048 feet.
Big Track. Nice.
A record time around the course in the Panoz school cars is 2 min 28 seconds. The students were doing 2:40 to 2:45. I believe I uncorked a 2:36 somewhere along the way, but my typical lap was 2:40 and the quicker guys pulled about 65 feet on me at the start-finish every lap, which I reckoned before to be worth half a second. What's the average speed at 2:40? That's 3.70 miles in 160 seconds. The average speed is 19,048 / 160 fps ~ 1905 / 16 ~ 476 / 4 ~ 119 fps, which is 119 x 15 / 22 mph, and that is (1190 + 595 ~ 1785) / 22 = 892.5 / 11. It's hard to divide by 11, so lets multiply instead. 80 mph by 11 would be 880, and that's not enough by 12.5. So, if we go with 81 mph by 11, namely 891, we're short by 1.5. A tenth of 11 will take care of some of that, so 81.1 by 11, namely 892.1, leaves us close enough. Now, doing the same distance in 2:28, or 148 seconds, yields an average speed of 19,048 / 148 ~ 4,762 / 37. Another tough divisor. Let's try 130 x 37 = 3700 + 1110 = 4810, too much by 48. But, we lucked out, it's obvious that 48 is about 1.30 x 37, so we get 130 - 1.30 = 128.7 fps. Now multiply that by 15 / 22: (1287 + 643.5) / 22 ~ 1930 / 22 = 965 / 11. 90 x 11 would be 990, too much by 25, which is a little more than 2 x 11. So 90 - 2 = 88 x 11 would be 880 + 88 = 968, too much by 3, so we'll reduce 88 by 0.3 x 11 to get 87.7. The average speed of a record-setting lap is 6.6 mph faster than our pitiful student laps! The difference is 12 seconds, so, as a rule of thumb, a second at 85 mph average is worth a little more than 1/2 an mph.
But, before we wander too far off topic, let's compare 2:40 to 2:40.5, since my contention from the beginning of this note is THAT difference can be accounted entirely to trail braking in four corners of this course: 2, 10, 13, and 15. Well, at 119 fps, average speed, half a second is about 60 feet, which is about 4 car lengths. Yep, there you have it: one car length per significant corner due to trail braking. Darn it, looks like I'll just have to go back there and keep trying, over and over again.